Answer:
• The data vary by a range of 16 years.
,
• The middle half of the data values vary by 7 years.
Step-by-step explanation:
The ages of the cousins in the Miller family are 2, 18, 6, 13, 8, 6, 11, and 4 years.
Arranging the ages in ascending order gives:
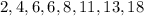
First, determine the range.
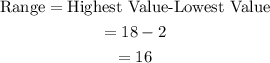
Next, determine the interquartile range:
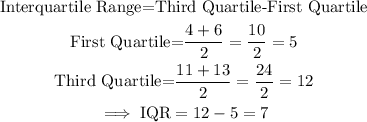
Therefore, we conclude that:
The data vary by a range of 16 years. The middle half of the data values vary by 7 years.