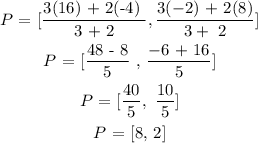The coordinates of point P along the directed line segment AB with A(-4,8) and B(16,-2) implies that the point P divides the line AB internally
Recall that the formular for the coordinates of a point that divides a line internally is given as
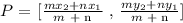
where m and n is the ratio of the internal division
Thus, we have