Question

The temperatue of a town months after January can be estimated by the function f(t) = - 26cos(pi/6 * t) + 48 .

Answer 1

`(2\left(78+72\pi\right))/(3\pi)=64.55211`

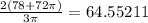
Step-by-step explanation

Given;

`f(t)=\left(-26cos\left((\pi)/(6)t\right)+48\right)\:`

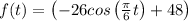
The average temperature from month 3 to month 6 ;

This will be the average value of the function over the interval (a,b);

Hence;

`\begin{gathered} (1)/(b-a)\int_a^bf(t)dt \\ \\ \end{gathered}`

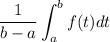
Substituting the values, we have;

`\begin{gathered} (1)/(6-3)\int _3^6\left(-26cos\left((\pi )/(6)t\right)+48\right)\:dt \\ (1)/(3)\int_3^6\left(-26cos\left((\pi)/(6)t\right)+48\right)\:dt \\ 2\left(-13\cos \left((\pi t)/(6)\right)+24\right) \\ \int _3^62\left(-13\cos \left((\pi t)/(6)\right)+24\right)dt \end{gathered}`

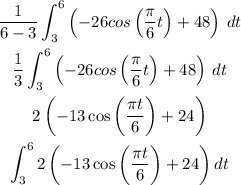
Take constant out;

`2\cdot \int _3^6-13\cos \left((\pi t)/(6)\right)+24dt`

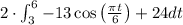
Apply sum rule;

`\begin{gathered} 2\left(-\int _3^613\cos \left((\pi t)/(6)\right)dt+\int _3^624dt\right) \\ \int_3^613\cos\left((\pi t)/(6)\right)dt=13\cdot\int_3^6\cos\left((\pi t)/(6)\right)dt \\ \end{gathered}`

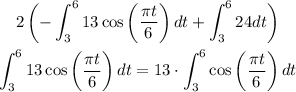
Using integral substitution;

`\begin{gathered} \:u=(\pi t)/(6) \\ (du)/(dt)=(\pi)/(6) \\ du=(\pi )/(6)dt \\ dt=(6)/(\pi )du \\ \int \cos \left(u\right)(6)/(\pi )du \end{gathered}`

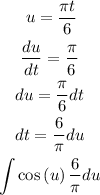
At t=3;

`\begin{gathered} (\pi 3)/(6) \\ (\pi )/(2) \end{gathered}`

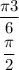
At t=6;

`(\pi6)/(6)=\pi`

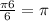
Now, we have;

`\begin{gathered} \int _{(\pi )/(2)}^(\pi )\cos \left(u\right)(6)/(\pi )du \\ 13\cdot \int _{(\pi )/(2)}^(\pi )\cos \left(u\right)(6)/(\pi )du \\ 13\cdot (6)/(\pi )\cdot \int _{(\pi )/(2)}^(\pi )\cos \left(u\right)du \\ 13\cdot (6)/(\pi )\left[\sin \left(u\right)\right]^(\pi )_{(\pi )/(2)} \\ (78)/(\pi )\left[\sin \left(u\right)\right]^(\pi )_{(\pi )/(2)} \\ 2\left(-\left(-(78)/(\pi )\right)+72\right) \\ 2\left((78)/(\pi )+72\right) \\ (2\left(78+72\pi \right))/(3\pi ) \end{gathered}`