Question

For the geometric sequence 4/3, 2/3, 1/3, 1/6, find the sum of S

Answer 1

The formula for a geometric sequence is:

`a_n=a_1r^((n-1))`

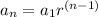
where a_1 is the first term of a sequence and r is the "coomon ratio"

We can see that theach term is half the previous term, thus r = 1/2

We can write:

`a_n=(4)/(3)\cdot((1)/(2))^((n-1))`

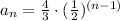
Now, that we know the sequence formula, we can write the sum of the sequence:

`\sum ^(n-1)_(k\mathop=0)(ar^k)=a((1-((1)/(2))^n)/(1-(1)/(2)))`

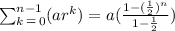
Thus:

`\sum ^(n-1)_{k\mathop{=}0}(ar^k)=2a(1-((1)/(2))^n)`