a. The growth of the fox population can be modeled by the following equation:
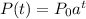
Where P0 is the initial value of the population, a is any number and t is the time in years.
To determine a we have to add 1 and the growth rate in decimal form, it means 0.09:
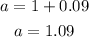
P0 has a value of 24200 which is the fox population in 2020.
The equation that models this situation is:
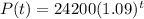
b. To find the fox population in 2028, replace t for 8 (number of years since 2020) and solve:
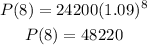
In 2028 there will be approximately 48220 foxes.