In this problem, we have a vertical parabola open downward
The vertex is a maximum
Remember that
The distance from the vertex to the directrix must be the same that the distance from the vertex to the focus
so
step 1
Find out the distance from the directrix to the focus
directrix -------> y=3
Focus ----> (1,1/2)
distance=3-1/2=2.5
2.5/2=1.25
the vertex is the midpoint between the focus and the directrix
so
the coordinates of the vertex are (1,0.5+1.25)
vertex (1,1.75)--------> vertex (1.7/4)
The equation in vertex form is given by

where
a is the leading coefficient
(h,k) is the vertex
(h,k)=(1,7/4)
substitute
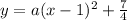
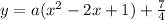
Remember that
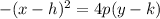
where
p is the focal distance
In this problem
p=1.25=5/4
substitute (h,k)=(1,7/4)
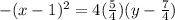
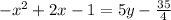
Isolate the variable y
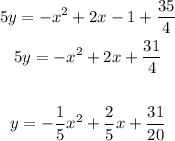
The answer is option C