Question

BEVERAGE)38SOUP)14NO BEVERAGE OR SOUP)7Jerald asked 50 students at his school cafeteria what they bought for lunch. He recorded his results in the table above. Use a Venn Diagram if necessary. If a student selected is selected at random what is: The probability they buy a beverage and soup?The probability they buy only a beverage or only soup?The probability they buy did not buy soup?

Answer 1

We have 50 students.

Out of the 50, 7 do not have beverage or soup.

Then, 50-7 = 43 students have beverage, soup or both.

We then, knowing that 38 had beverage and 14 had soup, so we can calculate using this rule:

`\begin{gathered} B\cup S=B+S-B\cap S \\ B\cap S=B+S-B\cup S \\ B\cap S=38+14-43 \\ B\cap S=9 \end{gathered}`

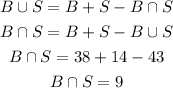
Then, we can draw a Venn diagram as:

We have calculated the number of students that only had beverage (group B) as the difference between the total number of students that had beverage, 38, and the number of students that had both beverage and soup, which is 9. The same can be done with the students that have only soup (group S).

a) We have to calculate the probability that they buy a beverage and soup.

We know that the probability can be expressed as the quotient between the success events and the possible outcomes.

In this case, we can express it as:

`P(B\cap S)=(B\cap S)/(N)=(9)/(50)=0.18`

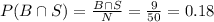
b) Now, we have to calculate the probability that the student had only beverage or only soup. We can calculate it as:

`P(B\text{ or }S)=(B+S-2\cdot(B\cap S))/(N)=(38+14-2\cdot9)/(50)=(34)/(50)=0.68`

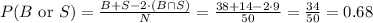
c) We can calculate the probability of the student not having soup as:

`P(\text{not S})=1-P(S)=1-(5)/(50)=1-0.1=0.9`

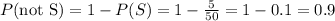
Answer:

a) 0.18

b) 0.68

c) 0.90