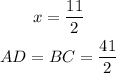In a parallelogram, opposite sides are equal. This means that AD=BC.
Since AD=3x+4 and BC=x+15, we have

If we move x to the left hand side as -x and 4 to the right hand side as -4, we obtain,
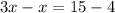
then, x is equal to
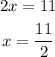
Now, we must substitute this values into AD and BC. We have for AD,
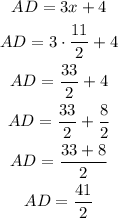
and for BC, we have
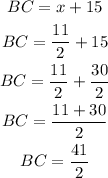
which is an expected result because AD=BC. However, its a checking for our computations.
In summary, the answers are: