Question

Angela is tossing a softball into the air with an underhand motion. The distance of the ball above her hand at anytime is given by the formula:h(t) = 80t 16t2 for 0 ≤ t ≤ 5where h(t) is the height of the ball (in feet) and t is the time (in seconds).At what times, t, is the ball in her hands? Note: there are 2 different times.The ball is in her hands at__ seconds. At what time, t is the ball at it's maximum height?The ball is at it's max height after__ seconds.How high, h, is the ball at it's maximum height?The ball's max height is__feet.

Answer 1

The function

`h(t)=80t-16t^2`

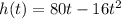
represents the height of the ball above the girl's hand, therefore, h = 0 represents the hand of the girl. The corresponding time for h = 0 are the solutions for the following equation:

`\begin{gathered} 0=80t-16t^2 \\ t(80-16t)=0 \end{gathered}`

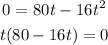
Since we have a product between two terms, equals to zero, one of the terms should be zero. The solutions are:

`\begin{gathered} t=0 \\ 80-16t=0\implies t=(80)/(16)=5 \end{gathered}`

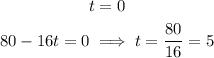
The ball is in her hands at 0 and 5 seconds.

The function that describes the height of the ball is a parabola that opens downwards, symmetric on its vertex. The vertex is located between the x-intercepts, and the vertex is the maximum point of the function. The maximum height happens at

`t=(5-0)/(2)=2.5`

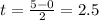
2.5 seconds.

Evaluating t = 2.5 on our function, we can find the maximum height.

`h(2.5)=80(2.5)-16(2.5)^2=100`

The maximum height is 100 feet.