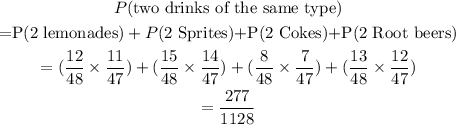Answer:
• (a)35/376
,
• (b)275/282
,
• (c)6/47
,
• (d)5/47
,
• (e)277/1128
Step-by-step explanation:
The number of each type of drink in the cooler is given below:
• Lemonades = 12
,
• Sprites = 15
,
• Cokes = 8
,
• Root beers = 13
The total number of drinks = 12+15+8+13=48
Part A
Since the selection is made without replacement:
• P(1st Sprite)=15/48
After the first selection, the number of Sprite reduces by 1, the total number of drinks also reduces by 1.
• P(2nd Sprite) = 14/47
Therefore, the probability that you get two cans of Sprite will be:
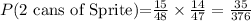
Part B (Probability that you do not get two cans of Coke)
• P(1st Coke)=8/48
,
• P(2nd Coke)=7/47
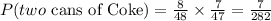
Therefore, the probability that you do not get two cans of Coke:
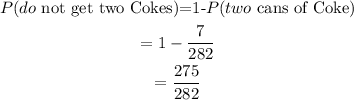
Part C (Probability that you get either two root beers or two lemonades)
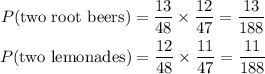
Since the joining word is OR, we add:
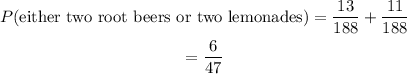
Part D (Probability that you get one can of Coke and one can of Sprite)
• P(one can of coke) = 8/48
,
• P(one can of Sprite)=15/47
Note that in this case, only the total reduces as the selection is made from different drinks.
Furthermore, we can either pick (Coke, Sprite) or (Sprite,Coke) in that order.
Therefore:
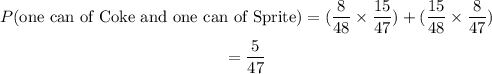
Part E
To get two drinks of the same type, we can pick 2 lemonades OR 2 Sprites OR 2 Cokes or 2 Root beers.
Thus: