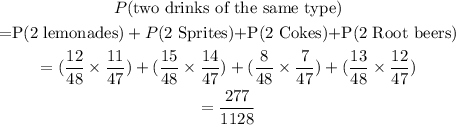Question

4. A large cooler contains the following drinks: 12 lemonades, 15 Sprites, 8 Cokes, and 13 root beers. You randomly pick two cans, one at a time (without replacement). Compute the following probabilities. (a) What is the probability that you get two cans of Sprite? (b) What is the probability that you do not get two cans of Coke? (c) What is the probability that you get either two root beers or two lemonades? (d) What is the probability that you get one can of Coke and one can of Sprite? (e) What is the probability that you get two drinks of the same type?

Answer 1

• (a)35/376

,

• (b)275/282

,

• (c)6/47

,

• (d)5/47

,

• (e)277/1128

Step-by-step explanation:

The number of each type of drink in the cooler is given below:

• Lemonades = 12

,

• Sprites = 15

,

• Cokes = 8

,

• Root beers = 13

The total number of drinks = 12+15+8+13=48

Part A

Since the selection is made without replacement:

• P(1st Sprite)=15/48

After the first selection, the number of Sprite reduces by 1, the total number of drinks also reduces by 1.

• P(2nd Sprite) = 14/47

Therefore, the probability that you get two cans of Sprite will be:

`P(2\text{ cans of Sprite)=}(15)/(48)*(14)/(47)=(35)/(376)`

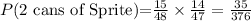
Part B (Probability that you do not get two cans of Coke)

• P(1st Coke)=8/48

,

• P(2nd Coke)=7/47

`P(two\text{ cans of Coke)}=(8)/(48)*(7)/(47)=(7)/(282)`

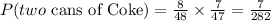
Therefore, the probability that you do not get two cans of Coke:

`\begin{gathered} P(do\text{ not get two Cokes)=1-}P(two\text{ cans of Coke)} \\ =1-(7)/(282) \\ =(275)/(282) \end{gathered}`

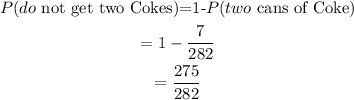
Part C (Probability that you get either two root beers or two lemonades)

`\begin{gathered} P(\text{two root beers)}=(13)/(48)*(12)/(47)=(13)/(188) \\ P(\text{two lemonades)}=(12)/(48)*(11)/(47)=(11)/(188) \end{gathered}`

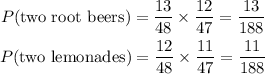
Since the joining word is OR, we add:

`\begin{gathered} P(\text{either two root beers or two lemonades)}=(13)/(188)+(11)/(188) \\ =(6)/(47) \end{gathered}`

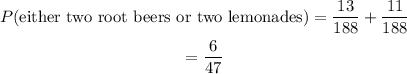
Part D (Probability that you get one can of Coke and one can of Sprite)

• P(one can of coke) = 8/48

,

• P(one can of Sprite)=15/47

Note that in this case, only the total reduces as the selection is made from different drinks.

Furthermore, we can either pick (Coke, Sprite) or (Sprite,Coke) in that order.

Therefore:

`\begin{gathered} P(\text{one can of Coke and one can of Sprite)}=((8)/(48)*(15)/(47))+((15)/(48)*(8)/(47)) \\ =(5)/(47) \end{gathered}`

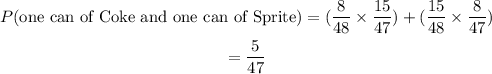
Part E

To get two drinks of the same type, we can pick 2 lemonades OR 2 Sprites OR 2 Cokes or 2 Root beers.

Thus:

`\begin{gathered} P(\text{two drinks of the same type)} \\ \text{=P(2 lemonades)}+P(2\text{ Sprites)+P(2 Cokes)+P(2 Root beers)} \\ =((12)/(48)*(11)/(47))+((15)/(48)*(14)/(47))+((8)/(48)*(7)/(47))+((13)/(48)*(12)/(47)) \\ =(277)/(1128) \end{gathered}`