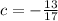Question

Hello, please help me with Question B in this question :)

Answer 1

Given: The vectors u, v, and w as-

`\begin{gathered} u=\begin{bmatrix}{2} & {} \\ {3} & {}\end{bmatrix} \\ v=\begin{bmatrix}{0} & {} \\ {1} & {}\end{bmatrix} \\ w=\begin{bmatrix}{4} & {} \\ {3} & {}\end{bmatrix} \end{gathered}`

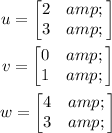
Required: To determine the value of c such that u+cw is orthogonal to u.

Step-by-step explanation: Two vectors are said to be orthogonal if their dot product is zero.

The vector u+cw is-

`\begin{gathered} u+cw=\begin{bmatrix}{2} & {} \\ {3} & {}\end{bmatrix}+c\begin{bmatrix}{4} & {} \\ {3} & {}\end{bmatrix} \\ =\begin{bmatrix}2+{4}c & {} \\ 3+{3}c & {}\end{bmatrix} \end{gathered}`

The dot product of two vectors of the form-

Now, taking the dot product of (u+cw) with u as follows-

`\begin{gathered} (u+cw)\cdot u=\begin{bmatrix}2+{4}c & {} \\ 3+{3}c & {}\end{bmatrix}\cdot\begin{bmatrix}{2} & {} \\ {3} & {}\end{bmatrix} \\ =4+8c+9+9c \end{gathered}`

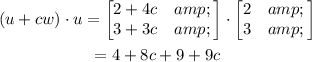
Now, the product will be zero if the vectors are orthogonal.

`\begin{gathered} 17c+13=0 \\ c=-(13)/(17) \end{gathered}`

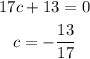
Final Answer: The value of c is-

`c=-(13)/(17)`