This problem is an example of the use of synthetic division. This can be used to divide polynomials when the divisor has the form (x-a), with a constant.
The steps in this algorithm are:
• 1. write the divisor as ,a,;
In this problem, a = -1.
• 2. write the dividend as the coefficients starting with the leading coefficient, in descending order of the terms' degrees;
In this problem, since the dividend is 3x³-2x²+3x-5, we should write:
3 -2 3 -5
• 3. bring down to the third row the leading coefficient;
In this problem, it's 3. So far, we obtained:
-1 | 3 -2 3 -5
3
• 4. multiply the leading coefficient by a and write the result in the second row;
In this problem, we have 3 * (-1) = -3. Thus, we obtain:
-1 | 3 -2 3 -5
-3
3
• 5. add the numbers on the second row:
-1 | 3 -2 3 -5
-3
3 -5
• 6. repeat steps 4 and 5 for the next coefficients:
-5 * (-1) = 5
3 + 5 = 8
8 * (-1) = -8
-5 - 8 = -13
-1 | 3 -2 3 -5
-3 5 -8
3 -5 8 -13
• 7. the obtained numbers on the third row are the coefficients of the quotient (with one degree less than the dividend), and the last number on the right is the remainder.
In this problem, we have:
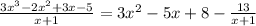
Therefore, the statement is True.