Question

I am trying to find an equation in vertex form by looking at a graph. how do I find the leading coefficient?

Answer 1

For a parabola, we have the vertex form as;

`a(x-h)^2+k`

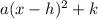
a is the leading coefficient, (-h,k) represents the equation of the vertex

By noting the roots of the equation, the value of x at which the curve crosses the y-axis, we have the roots.

Then, we can write the expanded form. By using the completing the square method, we can get the vertex form above. Writing the equation in the vertex form will give us the value of a

Take for example, we have the following quadratic equation;

`x^2\text{ + 6x + 8}`

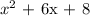
This graph will cross the x-axis at the points x = -2 and x = -4

So, to write this equation in the vertex form; we can divide the coefficient of x 6 by 2 and square it

We have this as ; (6/2) = 3^2 = 9

We can equate the equation to zero and add 9 to both sides

So we have;

`\begin{gathered} x^2\text{ + 6x + 8 + 9 = 9} \\ x^2+6x+9\text{ = 9-8} \\ x^2+6x\text{ + 9 = 1} \\ (x+3)^2\text{ = 1} \\ (x+3)^2-1\text{ = 0} \end{gathered}`

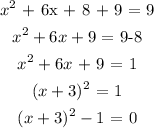
In this case, we can see that our a-value is 1 and that is the leading coefficient