Given:
The radius of the circle is 6.
Required:
We need to find the area of the pentagon.
Step-by-step explanation:
We divided the pentagon into five equal triangle parts.
Consider the triangle AOB.
Divide 360 degrees by 5 to find the angle AOB.
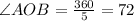
We need to find the angle AOC.
Divide the angle AOB by 2 since AC is the bisector.
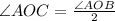
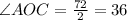
Consider the right angle triangle AOC.
We have the opposite side = AC and hypotenuse = AO=6.
Use sine formula.

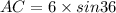

We know that AB=AC+BC and also AC+BC.
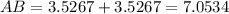
Use the Pythagorean theorem to find the apothem of the pentagon.
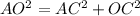
Substitute AO=6 and AC=3.5267 in the formula.
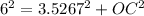
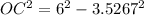
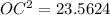
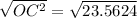
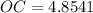
Use the area of the triangle formula for triangle AOB.
Height, OC=4.8541, and base AB=7.0534.
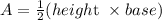
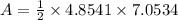
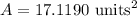
The area of the pentagon is 5 times A.
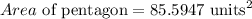
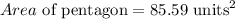
The area of the circle is
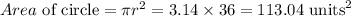
Subtract the area of the pentagon from the area of the circle,
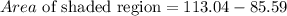
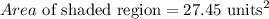
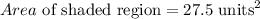
The shaded region is
Final answer:
The area of the shaded region is 27.5 square units.