Question

I seriously need help with this problem! I clearly don’t know what the heck I’m doing!

Answer 1

Given:

The radius of the circle is 6.

Required:

We need to find the area of the pentagon.

Step-by-step explanation:

We divided the pentagon into five equal triangle parts.

Consider the triangle AOB.

Divide 360 degrees by 5 to find the angle AOB.

`\angle AOB=(360\degree)/(5)=72\degree`

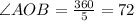
We need to find the angle AOC.

Divide the angle AOB by 2 since AC is the bisector.

`\angle AOC=(\angle AOB)/(2)`

`\angle AOC=(72\degree)/(2)=36\degree`

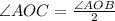
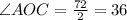
Consider the right angle triangle AOC.

We have the opposite side = AC and hypotenuse = AO=6.

Use sine formula.

`sin36\degree=(AC)/(6)`
`AC=6* sin36\degree`
`AC=3.5267`

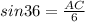
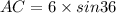
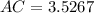
We know that AB=AC+BC and also AC+BC.

`AB=3.5267+3.5267=7.0534`

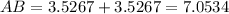
Use the Pythagorean theorem to find the apothem of the pentagon.

`AO^2=AC^2+OC^2`

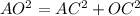
Substitute AO=6 and AC=3.5267 in the formula.

`6^2=3.5267^2+OC^2`

`OC^2=6^2-3.5267^2`
`OC^2=23.5624`
`√(OC^2)=√(23.5624)`

`OC=4.8541`

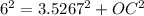
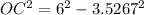
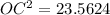
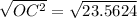
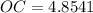
Use the area of the triangle formula for triangle AOB.

Height, OC=4.8541, and base AB=7.0534.

`A=(1)/(2)(heigh\text{t }* base)`

`A=(1)/(2)*4.8541*7.0534`

`A=17.11\text{90 units}^2`

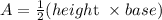
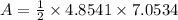
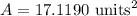
The area of the pentagon is 5 times A.

`Area\text{ of pentagon}=85.5947\text{ units}^2`

`Area\text{ of pentagon}=85.59\text{ units}^2`

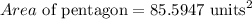
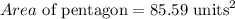
The area of the circle is

`Area\text{ of circle}=\pi r^2=3.14*36=113.04\text{ units}^2`

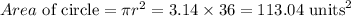
Subtract the area of the pentagon from the area of the circle,

`Area\text{ of shaded region}=113.04-85.59`

`Area\text{ of shaded region}=27.45\text{ units}^2`

`Area\text{ of shaded region}=27.5\text{ units}^2`

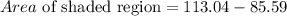
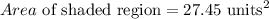
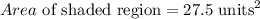
The shaded region is

Final answer:

The area of the shaded region is 27.5 square units.