Solution
For this case we have the proportion from the sample given
phat=0.72
And we have also the margin of error ME=0.04
And we want to find the likely interval so we can calculate the 95% confidence interval with the following formula:
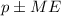
And replacing we got:
0.72 -0.04 =0.68
0.72 +0.04= 0.76
Then the confidence interval would be given by
0.68 < p < 0.76
For the second case we have:
For the second case we have the following:

Then we can replace in the margin of error formula and we got:
![ME=1.96\cdot\sqrt[]{(0.18\cdot(1-0.18))/(350)}=0.04](https://img.qammunity.org/2023/formulas/mathematics/college/k87d9nbldy9i7obtwji0vu3omjdtuje6df.png)
Then the interval would be:
0.18-0.04 =0.14
0.18+0.04=0.22
Then the answer is
B