Question

Listed below are foot lengths in inches for 11 randomly selected people taken in 1988. Find the standard deviation for the given sample data. Include appropriate units in the results. Are the statistics representative of the current population of all people?

Answer 1

Given:

`9.5,9.1,9.7,9.5,9.2,10.5,10.3,9.1,9.9,9.5,8.7`

Step-by-step explanation:

a) To find: Range

The range formula is,

`\begin{gathered} R=Largest\text{ value-Smallest value} \\ =10.5-8.7 \\ =1.8 \end{gathered}`

Therefore, the range of the data is 1.8.

b) To find: The standard deviation.

The formula is,

`\sigma=\sqrt{\frac{\sum_(i=1)^n(x-\bar{x})^2}{N-1}}`

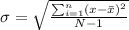
Here,

`\begin{gathered} Numbe\text{r of data, N=11} \\ Mean,\bar{x}=(\sum^x)/(N)=(105)/(11)\approx9.55 \end{gathered}`

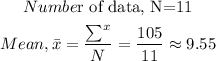
On substitution we get,

Therefore, the standard deviation for the given data is,

`\sigma\approx0.54`

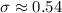
c) To find: Variance

Since the standard deviation is 0.54.

So, the variance becomes,

`\begin{gathered} \sigma=0.54 \\ Variance,\sigma^2\approx0.29 \end{gathered}`

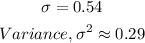
Final answer:

• The range of the data is 1.8.

,

• The standard deviation for the given data is 0.54.

,

• The variance for the given data is 0.29.