SOLUTION:
Case: Quadratic Application Word Problem
Given:
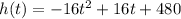
Required:
a. How long did it take for Jason to reach his maximum height?
b. What was the highest point that Jason reached?
c. What is Jason’s initial height?
Method:
Step 1: How long did it take for Jason to reach his maximum height?
To calculate this, we find the vertex

From here, the vertex is at (1/2, 484).
Hence it takes 1/2 a second to reach the maximum height
Step 2: What was the highest point that Jason reached?
Also, from the vertex, we get the highest height reached
The maximum height reached was 484 feet
Step 3: What is Jason’s initial height?
The initial height is gotten at the start of the motion, i.e. h(0) = ?

Hence the initial height was 480 feet
Final answer:
A) Time = 1/2 second
B) Maximum Height, H= 484 feet
C) Initial Height, H= 480 feet