Given: Square ASDF has diagonals ( line) AD and (line) SF
To Determine: The length of (line) SF if (line) AD=8x-5 and (line) SF= 4x+3
Solution:
The diagram below represents the given square
Given that
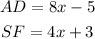
Please note that the diagonals of a square are equal. So, diagonal AD and diagonal SF are equal.
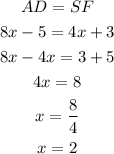
Therefore, line SF is
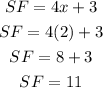
Hence, SF = 11