Given data:
* The mass of the car is m = 1250 kg.
* The initial velocity of the car is u = 0 m/s.
* The final velocity of the car is,
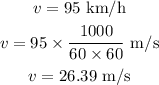
* The time taken by the car to increase its velocity is t = 8.5 s.
Solution:
(a). The acceleration of the car is,
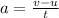
Substituting the known values,
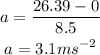
Thus, the acceleration of the car is 3.1 meters per second.
(b). By the kinematics equation, the displacement of the car is,
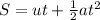
Substituting the known values,
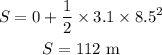
Thus, the displacement of the car is 112 meters.
(c). The work done by the car in 8.5 seconds is,
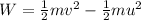
Substituting the known values,
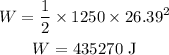
Thus, the work done by the car is 435270 J.
(d). The average power required for the motion is,
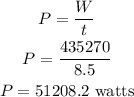
Thus, the power required for the given motion is approximately 51208 watts.