Question

A 1250 kg car accelerates uniformly from rest to a speed of 95 km/h in 8.5 s. (Hint: convert km/h to m/s)a. What is the car's acceleration? b. What is the car's displacement? c. How much work is done on the car during this 8.5 s interval? d. What average power is required to produce this motion?

Answer 1

Given data:

* The mass of the car is m = 1250 kg.

* The initial velocity of the car is u = 0 m/s.

* The final velocity of the car is,

`\begin{gathered} v=95\text{ km/h} \\ v=95*(1000)/(60*60)\text{ m/s} \\ v=26.39\text{ m/s} \end{gathered}`

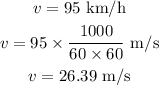
* The time taken by the car to increase its velocity is t = 8.5 s.

Solution:

(a). The acceleration of the car is,

`a=(v-u)/(t)`

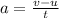
Substituting the known values,

`\begin{gathered} a=(26.39-0)/(8.5) \\ a=3.1ms^(-2) \end{gathered}`

Thus, the acceleration of the car is 3.1 meters per second.

(b). By the kinematics equation, the displacement of the car is,

`S=ut+\frac{1}{2^{}}at^2`

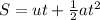
Substituting the known values,

`\begin{gathered} S=0+(1)/(2)*3.1*8.5^2 \\ S=112\text{ m} \end{gathered}`

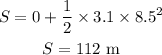
Thus, the displacement of the car is 112 meters.

(c). The work done by the car in 8.5 seconds is,

`W=(1)/(2)mv^2-(1)/(2)mu^2`

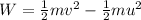
Substituting the known values,

`\begin{gathered} W=(1)/(2)*1250*26.39^2 \\ W=435270\text{ J} \end{gathered}`

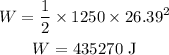
Thus, the work done by the car is 435270 J.

(d). The average power required for the motion is,

`\begin{gathered} P=(W)/(t) \\ P=(435270)/(8.5) \\ P=51208.2\text{ watts} \end{gathered}`

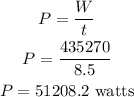
Thus, the power required for the given motion is approximately 51208 watts.