henSolution:
Given that;
An object is suspended by two cables attached at a single point.
The diagrammatic representation is shown below
For part A;
Writing the vector in component form
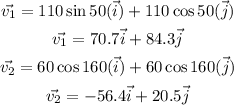
Hence, the answer is
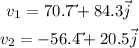
For part B;
Finding the dot product of the vectors
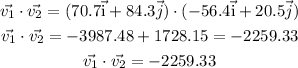
Hence, the dot product is
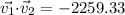
For part C
For the angles between vectors, using the dot product
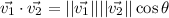
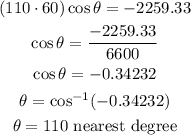
Hence, the angle between them is 110° (nearest degree)