Answer:
y = 2x -5. Option A is correct
Explanations:
The equation of a line in slope-intercept form is expressed as:

where:
m is the slope
b is the intercept
The slope of the line passing through the coordinates (4,3) and (2, -1) is given as:
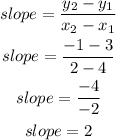
Determine the y-intercept" "b"
Using the coordinate point (4, 3) and m = 2
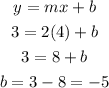
Determine the required equation
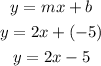
Hence the equation of the line that passes through (4,3) and (2, -1) is y = 2x -5