Question

a person invests 5500 dollars in the bank. the bank pays 4.25% interest compounded quarterly. to the nearest tenth of a year, how long must a person leave the money in the bank until it teaches 8600 dollars?

Answer 1

Step 1. The information that we have is:

-The initial investment, which will be the principal P:

`P=5,500`

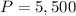
-The interest rate r which we will represent as a decimal number:

`\begin{gathered} r=4.25/100 \\ r=0.0425 \end{gathered}`

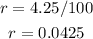
-The investment is compounded quarterly, this is 4 times per year:

`n=4`

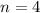
Required: Find the time in years it will take for the amount to be $8,600.

This final amount is A:

`A=8,600`

Step 2. Once we have defined all of our values, we use the compound interest formula:

`A=P(1+(r)/(n))^(nt)`

And substitute the known values:

`8,600=5,500(1+(0.0425)/(4))^(4t)`

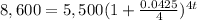
Step 3. To simplify, we solve the operations in the pair of parentheses:

`\begin{gathered} 8,600=5,500(1+0.010625)^(4t) \\ \downarrow \\ 8,600=5,500(1.010625)^(4t) \end{gathered}`

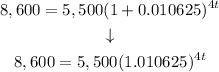
Then, divide both sides by 5,500:

`\begin{gathered} (8,600)/(5,500)=(5,500(1.010625)^(4t))/(5,500) \\ \downarrow \\ 1.563636364=(1.010625)^(4t) \end{gathered}`

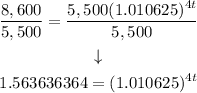
Step 4. Since we need to find the value of t which is in the exponent of the equation, we apply the logarithm to both sides of the equation:

`log(1.563636364)=log(1.010625)^(4t)`

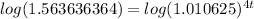
And due to the following property of logarithms:

`log(x^n)=nlog(x)`

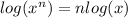
The expression can be written as follows:

`log(1.563636364)=4t* log(1.010625)`

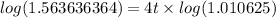
Step 5. Solving for t:

`\begin{gathered} 4t=(log(1.563636364))/(log(1.010625)) \\ \downarrow \\ 4t=42.29502968 \\ \downarrow \\ t=(42.29502968)/(4) \\ \downarrow \\ t=10.57375742 \end{gathered}`

Rounding the time to the nearest tenth:

`t=10.6`

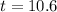
The time is 10.6 years.

Answer:

10.6 years