Question

I need help with this question for my exam practice, please. pi = 3.14

Answer 1

28.095 cm^2

Step-by-step explanation:

To determine the area of the given shape, we have to determine the area of the complete rectangle, then subtract the areas of each of the cut-out semi-circles as seen below;

From the shape, let's determine the length and width of the rectangle;

Length(l) = 2 cm + 5 cm + 2 cm = 9 cm

Width(w) = 1 cm + 4 cm + 1 cm = 6 cm

So the area of the complete rectangle will be;

`\begin{gathered} A_r=l\cdot w=9\cdot6=54cm^2 \\ \text{where;} \\ A_r=\text{ Area of the complete rectangle} \end{gathered}`

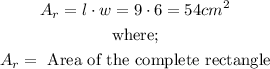
Let's now determine the area of the top semi-circle given that the radius is 2cm (radius = diameter/2 = 4/2 = 2cm);

`\begin{gathered} A_{\text{tsc}}=(\pi r^2)/(2)=(3.14(2)^2)/(2)=(3.14\cdot4)/(2)=(12.56)/(2)=6.28cm^2 \\ \text{where;} \\ A_{\text{tsc}}=\text{Area of top semi-circle} \end{gathered}`

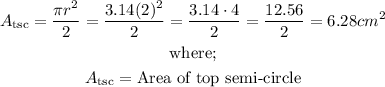
Given that the two semi-circles by the side of the rectangle have the same radius(r) which is 2.5cm (r = diameter/2 = 5/2 = 2.5cm), let's go ahead and determine their area;

`\begin{gathered} A_{\text{ssc}}=2((\pi r^2)/(2))=\pi r^2=3.14\cdot(2.5)^2=3.14\cdot6.25=19.625cm^2 \\ \text{where;} \\ A_{\text{ssc}}=\text{Area of side semi-circles} \end{gathered}`

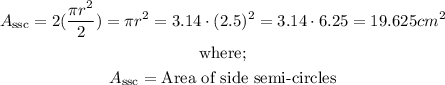
So the area of the shape will be;

`\begin{gathered} A=A_r-A_{\text{tsc}}-A_{\text{ssc}}=54-6.28-19.625=28.095cm^2 \\ \end{gathered}`

Therefore, the area of the shape is 28.095 cm^2