Part A
we have the equation
(x-13)^2+(y-4)^2=16
Rewrite as
(x-13)^2+(y-4)^2=4^2
so
The center of the circle is the point (13,4)
The radius of the circle is 4 units
using a graphing tool
Part B
Remember that
If an ordered pair lies on the circle, then the ordered pair must satisfy the equation of the circle
so
Verify each ordered pair
Hunter (11,4)
For x=11 and y=4
substitute in the equation of the circle
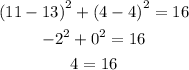
Is not true
so
Hunter is not in the spotlight
Joe (8,5)
x=8 and y=5
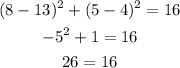
Is not true
so
Joe is not in the spotlight
Mason (15,5)
x=15 and y=5
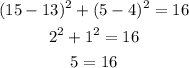
Is not true
Mason is not in the spotlight