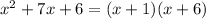A quadratic equation can be rewritten as
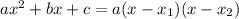
where x1 and x2 represents the roots of the quadratic equation.
To find those roots we can use the quadratic equation. Given a quadratic equation with the following form

its roots are given by
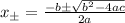
In our first quadratic equation, we have
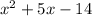
therefore, its roots are
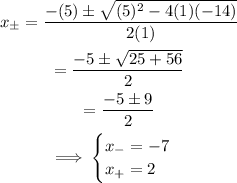
Then, this quadratic expression can be factorized as

Using the same process for the other expression, we have