Question

A survey was conducted to determine how many movies were seen in one month among the 26 students in Mrs. Hampton’s sixth-grade class. The results are shown in the dot plot below.c) Calculate the measures of spread for Mrs. Hampton's class data. Justify your response by describing the process used to find each measure.d) Which is a better measure of spread: range or interquartile range? Why?e) What does the value of the mean absolute deviation tell you about the spreadof the data?

Answer 1

c. In calculating the measures of spread, we have several ways. We have range, quartile, interquartile range, variance, standard deviation, and mean absolute deviation.

1. Range is the difference between the highest value and the lowest value. In the data, the lowest value is 0 movies while the highest value is 10 movies. Hence, range = 10.

`\begin{gathered} \text{Range}=\max -\min \\ \text{Range}=10-0 \\ \text{Range}=10 \end{gathered}`

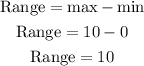
2. Quartile divide an ordered data set into 4 equal parts.

Quartile 1 or lower quartile - 25th percentile

Quartile 2 or second quartile - 50th percentile or the median

Quartile 3 or upper quartile - 75th percentile

To solve this, let's list down in order the data set.

0, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10.

The 25th percentile of this 26 data would be the data between the 6th and 7th place. Based on the data, it is 5. (Q1)

The 50th percentile would be the data found in the middle and that is the data between 13th and 14th place. It is 6. (Q2)

Lastly, the upper quartile would be the data between 19th and 20th place and that is 8. (Q3)

To summarize, Q1 = 5, Q2 = 6, and Q3 = 8.

3. Interquartile range is the difference between Q3 and Q1.

`\begin{gathered} \text{IQR}=Q3-Q1 \\ \text{IQR}=8-5 \\ \text{IQR}=3 \end{gathered}`

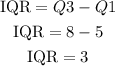
Interquartile range = 3.

4. Standard deviation measures the spread of the data around the center. The smaller the standard deviation is, the closer the data are around the mean.

The formula for this is:

`SD=\sqrt[]{\frac{\sum ^(26)_(i\mathop=1)f(X_i-\bar{X})^2}{N}}`

To be able to calculate the standard deviation, we need to solve for the mean first. In this set of data, the mean is approximately 6.35.

Let's create a table for this.

Now that we have the summation of the square of the difference mean and the data, let's plug it in to the formula. Remember too that N = 26 or the sample size.

`SD=\sqrt[]{(139.885)/(26)}\approx2.32`

Hence, the standard deviation is approximately 2.32. This means that, in general, the data are 2.32 points deviated from the center of the data set.

5. On the other hand, variance is the square of the standard deviation.

`\begin{gathered} Variance=(SD)^2 \\ Variance=2.32^2\approx5.38\text{ } \end{gathered}`

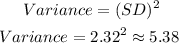
Variance = 5.38

6. Mean absolute deviation is the average distance between each data value and the mean. To solve this, we have the formula below.

`\text{MAD}=\frac{\sum ^(10)_(x\mathop=1)f|x-\bar{x}|}{N}`

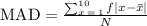
Let's make a table again to solve the numerator part of the formula.

Hence, the summation of the absolute value of the difference between mean and the raw data multiplied to the frequency is 50.4. Let's plug it in to the formula for MAD as well as N =26.

`\text{MAD}=(50.4)/(26)\approx1.94`

The mean absolute deviation of the given data is approximately 1.94.

d. Interquartile range is a better measure of spread compared to range because interquartile range is not affected by the outliers like extremely low value/high values in the data set. For example, in the data set, we have an extremely low value which is zero and range is affected by this.

e. With an MAD of 1.94, this means that the average distance of each data and the mean is 1.94. With this small distance, we can say that the data are close around the mean.