Question

This table models a linear function.x −8 −4 4 8y −1 0 2 3Enter the coordinates of the y-intercept in the boxes.$$ The first person to answer gets 100 points!!!!

Answer 1

So we have a table that defines the following four points:

`(-8,-1),(-4,0),(4,2),(8,3)`

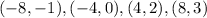
In order to find the y-intercept we should found the equation of the line first. This equation in point-slope form is:

`y=mx+b`

Where m and b are parameters that we must find. Since we are looking for the line that passes through the points defined by the table then they are all solutions to the equation. This means that if we take a point and replace x and y in the equation with the coordinates of the point we can build an equation for m and b. Then we pick points (-4,0) and (4,2) and we build 2 equations:

`\begin{gathered} 0=-4m+b \\ 2=4m+b \end{gathered}`

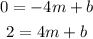
Now we take the first equation and we add 4m to both sides:

`\begin{gathered} 0+4m=-4m+4m+b \\ 4m=b \end{gathered}`

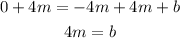
And then we replace this expression in place of b in the second equation:

`\begin{gathered} 2=4m+b=4m+4m \\ 2=8m \end{gathered}`

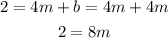
And we divide both sides by 8:

`\begin{gathered} (2)/(8)=(8m)/(8) \\ (1)/(4)=m \end{gathered}`

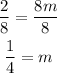
Then b is given by:

`\begin{gathered} 4\cdot m=4\cdot(1)/(4)=b \\ b=1 \end{gathered}`

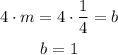
Then the equation of the line we are looking for is:

`y=(x)/(4)+1`

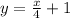
And the y-intercept is given when x=0 so we can find y:

`\begin{gathered} y=(0)/(4)+1=1 \\ y=1 \end{gathered}`

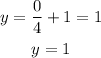
Then the coordinates of the y-intercept and answer to this problem are (0,1).