1 Answer

Phaylon · Answer 1 · 2023-01-07T20:07:20+0000

The formula for the area of a sector of a circle is:

$A=(\theta)/(360)*\pi r^2$

We want to find the area of the blue sector.

First, let's find the angle of the sector. This angle and angle 84 are in a straight line. Thus, we can say:

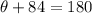
$\theta+84=180$

Where θ is the angle of the sector.

Let's solve for θ:

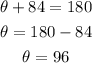
$\begin{gathered} \theta+84=180 \\ \theta=180-84 \\ \theta=96 \end{gathered}$

We also recognize that BD is the diameter and BA is the radius.

We know

Radius is HALF of Diameter.

Given,

Diameter = 6

Radius = 6/2 = 3

Now, let's calculate the area of the sector:

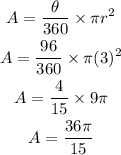
$\begin{gathered} A=(\theta)/(360)*\pi r^2 \\ A=(96)/(360)*\pi(3)^2 \\ A=(4)/(15)*9\pi \\ A=(36\pi)/(15) \end{gathered}$

Rounded to 2 decimal places,

Answer

Please log in or register to add a comment.