Question

I need help asap so I can turn in

Answer 1

`\begin{gathered} 1:\text{ }D \\ 2:\text{ }B \\ 3:\text{ }A \\ 4:\text{ }C \end{gathered}`

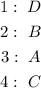
Step-by-step explanation:

Let's see each expression:

The expression 1 is:

`(3+5i)-(10+4i)`

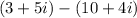
We know that in order to add or rest complex numbers, the real part goes with the real part an the same with the imaginary part.

Then:

`(3+5\imaginaryI)-(10+4\imaginaryI)=(3-10)+(5i-4i)=-7+i`

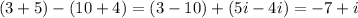
Now, let's look the expression D:

`D.(1+2i)(-1+3i)`

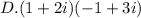
And solve:

`(1+2i)(-1+3i)=1(-1)+1\cdot3i+2i(-1)+2i\cdot3i=-1+3i-2i+6i^2=-1-6+i=-7+i`

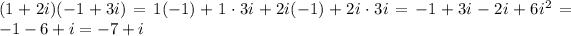
Expressions 1 and D are the same.

For expression 2:

`2.(2+4i)(2-4i)`

Let's solve it. We can see that the expression is a difference of squares: