We need to clear first in one equation any of the variables:
Lest take the first one:
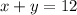

We replace this value of x in the other equation:


then organizing we have
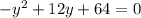
Using the quadratic equation we obtain:
![y=\frac{-12\pm\sqrt[]{12^2-4(-1)(64)}}{2(-1)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/mv4wvggu3c809einbtu0bwk8g8eu1ybya5.png)
![y=\frac{-12\pm\sqrt[]{144+256}}{-2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/y2yo4mc6r8s0vsc8flq6wevu2xc8bciq04.png)
![y=\frac{-12\pm\sqrt[]{400}}{-2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ytc716wpwamv8ki2l6xhq7qqej07jnmqdo.png)
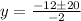
we have two possible solution, one with the addition and one with the subtration

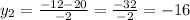
Using that values in the first equation when we clear the x:
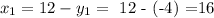
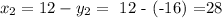
So if we can see those values in the equation x • y = -64
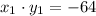

If you try to do this multiply with x2 y y2 it will be a different number s
The answer is X= 16 y Y= - 4