Question

X + y = 12x • y = -64

Answer 1

We need to clear first in one equation any of the variables:

Lest take the first one:

`x+y=12`
`x=12-y`

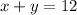
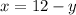
We replace this value of x in the other equation:

`(12-y)\cdot\text{ y = -64}`
`12y-y^2=\text{ -64}`

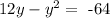
then organizing we have

`-y^2+12y+64=0`

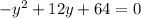
Using the quadratic equation we obtain:

`y=\frac{-12\pm\sqrt[]{12^2-4(-1)(64)}}{2(-1)}`
`y=\frac{-12\pm\sqrt[]{144+256}}{-2}`
`y=\frac{-12\pm\sqrt[]{400}}{-2}`
`y=(-12\pm20)/(-2)`

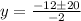
we have two possible solution, one with the addition and one with the subtration

`y_1=(-12+20)/(-2)=(8)/(-2)=-4`

`y_2=(-12-20)/(-2)=(-32)/(-2)=-16`

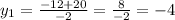
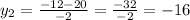
Using that values in the first equation when we clear the x:

`x_1=12-y_1=\text{ 12 - (-4) =16}`
`x_2=12-y_2=\text{ 12 - (-16) =28}`

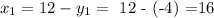
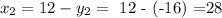
So if we can see those values in the equation x • y = -64

`x_1\cdot y_1=-64_{}`
`16\cdot(-4)=-64`

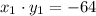
If you try to do this multiply with x2 y y2 it will be a different number s

The answer is X= 16 y Y= - 4