We have the following:
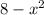
A polynomial is an algebraic expression formed by the sum of a finite number of monomials, therefore, Yes, it is a polynomial function
A)
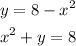
B)
The degree of the polynomial is 2, because the highest exponent of the polynomial
C)
It is a heterogeneous polynomial since it is a polynomial in which not all its terms are not of the same degree.
D)
The main coefficient is the coefficient that accompanies the one with the highest degree, therefore, would be -1