Question

What is the minimum speed with which a meteor strikes the top of Earth’s stratosphere (about 46.0 km above the surface), assuming that the meteor begins as a bit of interplanetary debris far from Earth and stationary relative to Earth? Assume that the drag force is negligible until the meteor reaches the stratosphere. Mass of Earth is 5.974 × 1024 kg; radius of Earth is 6.371 × 106 m; and gravitational constant is 6.674 × 10−11 N·m2/kg2. km/s

Answer 1

We are asked to determine the velocity of a mass that hits the Earth's atmosphere. To do that we need to do a balance of energy. The kinetic energy of the meteor must be equal to the energy of the gravitational field of the earth at the point where the meteor hits. This is written as:

`(1)/(2)mv^2=\frac{\text{GMm}}{R^{}}`

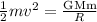
Where:

`\begin{gathered} m=\text{ mass,}\lbrack kg\rbrack \\ v=\text{ velocity,}\lbrack(m)/(s)\rbrack \\ G=\text{ gravitational constant} \\ M=\text{ Earth's mass} \\ R=\text{ distance from the center of the Earth where the meteor hits,}\lbrack m\rbrack \end{gathered}`

Now, we can cancel out the mass "m" in the equation:

`(1)/(2)v^2=(GM)/(R)`

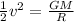
Now, we solve for the velocity, first by multiplying both sides by 2:

`v^2=(2Gm)/(R)`

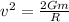
Now, we take the square root on both sides:

`v=\sqrt[]{(2Gm)/(R)}`

Now, before we substitute the values we need to convert the 46 km to meters. To do that we use the following conversion factor:

Now, we multiply the distance by the conversion factor:

The distance "R" is equal to the radius of the Earth plus the 46000 meters above the surface where the meteor strikes. Substituting the values we get:

Solving the operations:

`v=11147.4(m)/(s)`

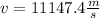
Since we are required to express the answer in km/s, we will convert the meters into kilometers:

Therefore, the speed of the meteor is 11.15 km/s