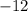Answer:
The average rate of change for the function between the given interval is;
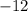
Step-by-step explanation:
The average rate of change for the given function;
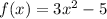
Between the interval;

can be calculated as;
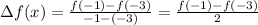
The value of f(x) at x=-1 and -3 are;
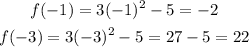
So;

Therefore, the average rate of change for the function between the given interval is;