To solve this question, we are given an equation:
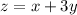
With the constraints:
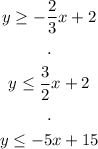
We need to find the vertices of the region to find the values of x.
The next step is to equate the equations by pairs:
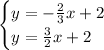
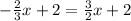
And solve:
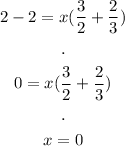
Now, we can find y:
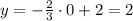
This vertex is: (0, 2)
Now, the next pair:
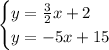
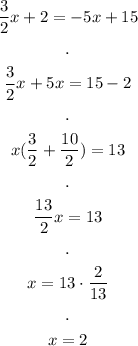
And find the value of y:
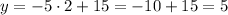
The coordinates of this vertex are: (2, 5)
Finally, the last pair:
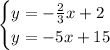
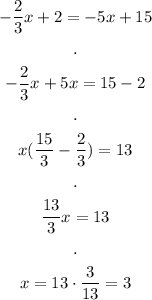
Now find y:
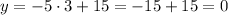
The coordinates of this vertex are: (3, 0)
Now, we need to evaluate z on those vertices to find the maximum and minimum values of z.
First vertex (0, 2):
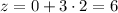
Second vertex (2, 5):
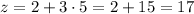
Third vertex (3, 0)
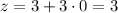
The answer is:
Maximum value of z: 17
Minimum value of z: 3