The given information is:
- The vertex of the parabola is (6,2)
- The equation of its directrix is y=0
As the directrix is y=0, this means we have a vertical parabola.
The standard form of the equation of a vertical parabola is given by:
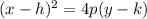
Where (h,k) is the vertex of the parabola, and p is given by the directrix equation:

Let's start by finding p:
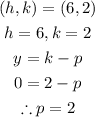
Now, replace the known values and find the equation:

The answer is above.