The first quartile is the number in between the lowest number of a data set and the median. To find it, I would use a Z table as shown below
The z score that corresponds to 0.25 is -0.67 on the table above.
Using the equation of z-score below
![\begin{gathered} z=(x-\mu)/(\sigma) \\ \text{Where}\mu=\operatorname{mean},\sigma=s\tan dard\text{ deviation} \end{gathered}]()
Where x is the value we're looking for and σ and μ are the standard deviations and the mean given in the problem.
Given that the mean is 100.4 and the standard deviation is 19.7, make x the subject of the z-score formula and substitute for the mean and standard deviation as shown below
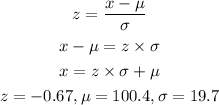
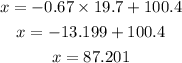
Hence, the first quartile is 87.201