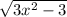Drawing a diagram of the triangle we have
Let a be the length of the perpendicular height of the triangle, then we can solve it using the Pythagorean Theorem
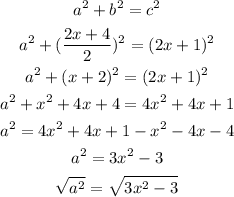
Therefore, the length of the perpendicular height of the triangle can be given in the expression