To determine vector R we need to construct vectors A and B.
From the diagram we know that vectors A and B are:
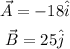
Then vector R is:

Now, that we have that we know that the magnitude of a vector is given as:
![R=\sqrt[]{R^2_x+R^2_y}^{}_{}](https://img.qammunity.org/2023/formulas/physics/college/pga3937c0xbsl2xw3ix6gnfe3o3wrh7bjf.png)
where Rx and Ry are the components in each direction. With this in mind we have that the magnitude is:
![\begin{gathered} R=\sqrt[]{(-18)^2+(25)^2} \\ R=30.81 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/z9xrfaq9nbz0wc1blq5qr09s5zf1xrg3s8.png)
Therefore, you are 30.81 meters from the starting point.
Now, to find the the direction (that is angle theta) we can use the following:
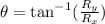
Now, from the figure we notice that we need to use the absolute value of each component (this means they both have to be positive) then we have:
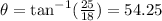
Therefore the direction is W52.25°N (this means that we measure the angle from west to north, as in the figure)