Question

The length of a rectangle is 6 meters less than twice its width. If the area of the rectangle is 308 m², what are its dimensions?A. 7 meters by 44 metersB. 11 meters by 28 metersC. 75 meters by 42 metersD. 14 meters by 22 meters

Answer 1

We have a reactanlge whose width and length are defined as follows:

Width ( w ) = x

Length ( L ) = 2x - 6

We have defined the unknown dimension of the rectangle width as ( x ). Then length of the rectangle is expressed in terms of the width as 6 meters less than twice of width.

The two dimensions ( width and length ) have been defined above. We will go ahead and express the area of a rectangle using the two dimension defined as follows:

`\begin{gathered} \text{Area = w}\cdot L \\ \text{Area = }x\cdot(2x-6) \end{gathered}`

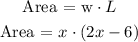
The area of the rectangle is given to us as:

`\begin{gathered} \text{Area = 308 = 2x}^2\text{ - 6x} \\ 2x^2-6x\text{ - 308 = 0} \\ x^2\text{ -3x - 154 = 0} \end{gathered}`

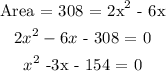
What we expressed above is a quadratic equation for the width ( w ) of the rectangle that satisfies the corresponding relationship with length ( L ) and Area ( A = 308 m^2 ).

To determine the width ( w ) with above conditions, we will have to solve the derived quadratic equation in ( x ).

The general formula for solving a quadratic equation is expressed for a form:

`\begin{gathered} ax^2+bx\text{ + c = 0} \\ a,b,c\text{ are constants} \end{gathered}`

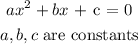
The general formula gives us:

`x\text{ = }(-b\pm√(b^2-4\cdot a\cdot c))/(2\cdot a)`

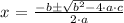
So for our quadratic equation we have:

`\begin{gathered} a\text{ = 1, b = -3, c = -154} \\ x\text{ = }(3\pm√((-3)^2-4\cdot(1)\cdot(-154)))/(2\cdot(1))\text{ = }\frac{3\pm\sqrt{9\text{ +616 }}}{2} \\ x\text{ = }(3\pm√(625))/(2)\text{ = }(3\pm25)/(2) \\ x\text{ = }(3+25)/(2)\text{ , }(3-25)/(2) \\ x\text{ = }(28)/(2)\text{ , }(-22)/(2) \\ x\text{ = 14 , -11} \end{gathered}`

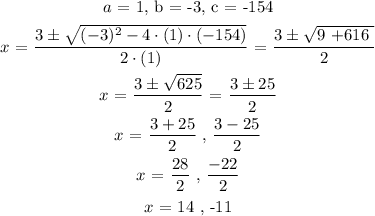
We have two values from the quadratic equation for the width of the rectangle. However, all dimensions only perceives positive values as its a length which is only defined by positive real numbers. Hence,

`\textcolor{#FF7968}{w}\text{\textcolor{#FF7968}{ = x = 14 m}}`

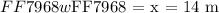
We will use the relationship between width ( w ) and length ( L ) to determine the length wise dimension of the rectangle as follows:

`\begin{gathered} L\text{ = 2}\cdot(14)\text{ - 6} \\ L\text{ = 28 - 6} \\ \textcolor{#FF7968}{L}\text{\textcolor{#FF7968}{ = 22 m}} \end{gathered}`

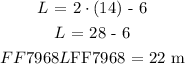
Therefore, with the given condtions for the rectangle the width x length dimension of the trianglw would be expressed as:

`\begin{gathered} w\text{ x L} \\ \textcolor{#FF7968}{(14}\text{\textcolor{#FF7968}{ x 22 ) m }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Option ( D )}} \end{gathered}`