Question

Siobhan is making 12 lbs of trail Mix with raisins and almonds. Raisins cost 5.10 per lb and almonds cost 3.30 per lb. How many lbs of raisins and how many lbs of almonds should siobhan use for the mixture to cost 3.90 per lb to make blank lbs of raisins and blank lbs of almonds?

Answer 1

r: Amount of raisins used (in lbs)

a: Amount of almonds used (in lbs)

Total lbs used: 12

Raisins cost: 5.10 per lb

Almonds const: 3.30 per lb

From the problem, we know that:

`a+r=12...(1)`

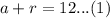
If the mixture cost 3.90 per lb, and we have 12 lbs of the mixture, then the total cost is:

`12\cdot3.90=46.8`

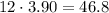
Then, we have another equation:

`5.1r+3.3a=46.8...(2)`

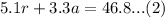
From equation (1):

`a=12-r...(3)`

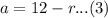
Using (3) on (2):

`5.1r+3.3(12-r)=46.8`

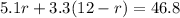
Solving this equation for r:

`\begin{gathered} 5.1r+39.6-3.3r=46.8 \\ 1.8r=7.2 \\ \Rightarrow r=4 \end{gathered}`

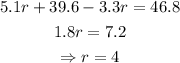
Using this result on (3):

`\begin{gathered} a=12-4 \\ \\ \Rightarrow a=8 \end{gathered}`

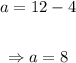
Answer:

Siobhan used 8 lbs of almonds and 4 lbs of raisins.