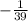Question

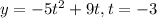
Find the Slope of the normal to the functiony = -5t^2+ 9t at t = -3

Answer 1

Given

`y=-5t^2+9t,t=-3`

Find

The slope of the normal

Step-by-step explanation

to find the slope we need to differentiate the function with respect to t.

`\begin{gathered} y=-5t^2+9t \\ (dy)/(dt)=-10t+9 \end{gathered}`

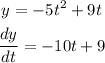
Slope = dy/dt

now, slope at t = -3

`\begin{gathered} (dy)/(dt)_(t=-3) \\ -10*(-3)+9 \\ 30+9 \\ 39 \end{gathered}`

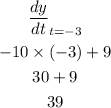
as we know that the slope of normal is perpendicular to tangent. hence the slope of normal is given by

slope of tangent * slope of normal = -1

so, slope of normal =

`-(1)/(39)`

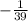
Final Answer

slope of normal =

`-(1)/(39)`