Question

Solve for a if the line through the two given points has the given slope.(a, -1) and (4, - 4), m = 3a = ?

Answer 1

To answer this question, we have to use the concept of a slope of a line. The slope of a line is given by the next formula:

`m=(y_2-y_1)/(x_2-x_1)`

Now, we have that the two points are (a, -1) and (4, -4), and we can label them as follows:

• (a, -1) ---> x1 = a, y1 = -1

,

• (4, -4) ---> x2 = 4, y2 = -4

We already know that m = 3. Then we have:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ 3=(-4-(-1))/(4-a) \\ 3=(-4+1)/(4-a) \\ 3=(-3)/(4-a) \end{gathered}`

Now, if we multiply both sides of the equation by (4 - a), we have:

`\begin{gathered} (4-a)\cdot3=(4-a)\cdot(-3)/((4-a)) \\ (4-a)\cdot3=((4-a))/((4-a))\cdot(-3)\Rightarrow((4-a))/((4-a))=1 \\ (4-a)\cdot3=-3 \end{gathered}`

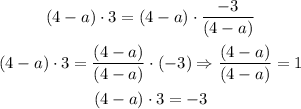
We need to apply here the distributive property. Then we have:

`\begin{gathered} 4\cdot3+(-a)(3)=-3 \\ 12-3a=-3 \end{gathered}`

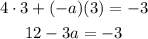
Now, we have to subtract 12 from both sides of the equation, and then we need to divide the result by -3 as follows:

`\begin{gathered} 12-12-3a=-3-12 \\ -3a=-15 \\ (-3a)/(-3)=(-15)/(-3) \\ a=5 \end{gathered}`

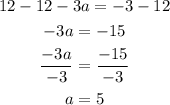
We can check this result if we substitute the result into the original equation as follows:

x1 = 5, y1 = -1

x2 = 4, y2 = -4

`\begin{gathered} 3=(-4-(-1))/(4-5)_{} \\ 3=(-4+1)/(-1) \\ 3=(-3)/(-1) \\ 3=3\Rightarrow This\text{ is True.} \end{gathered}`

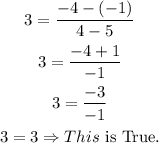
In summary, therefore, the value for a is equal to 5, a = 5.