Question

Graph the linear equation -x+5y=5

Answer 1

Given the linear equation;

`-x+5y=5`

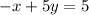
We'll begin by re-writing in the slope-intercept form as follows;

`\begin{gathered} \text{The equation in slope-intercept form is;} \\ y=mx+b \\ -x+5y=5 \\ \text{Add x to both sides} \\ 5y=x+5 \\ \text{Divide both sides by 5} \\ (5y)/(5)=(x+5)/(5) \\ y=(x)/(5)+(5)/(5) \\ y=(x)/(5)+1 \end{gathered}`

To graph the linear equation, we shall use the intercepts method. That is plot two points where x = 0 and y = 0.

`\begin{gathered} \text{When x}=0 \\ y=(0)/(5)+1 \\ y=1 \\ \text{Therefore we have;} \\ (0,1) \\ \text{Similarly, when y}=0 \\ 0=(x)/(5)+1 \\ (x)/(5)=-1 \\ \text{Cross multiply and we'll have;} \\ x=-5 \\ \text{Therefore, we have;} \\ (-5,0) \end{gathered}`

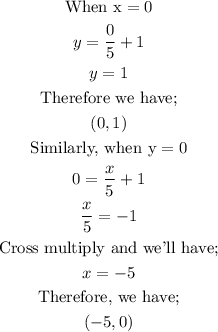
With these two points we now have the graph;