The given expression is:
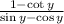
It is required to simplify to a single trigonometry function using sin y and cos y.
To do this, use trigonometry identity:
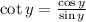
Hence, the expression can be written as:
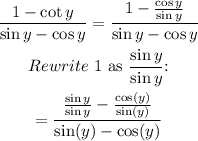
Simplify the numerator:
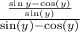
Simplify the expression further:
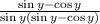
Cancel out common factors in the denominator and numerator:
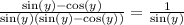
Hence, the required answer is 1/sin(y).