Question

No one has been able to help with this and get the right answer

Answer 1

The given expression is:

`(1-\cot y)/(\sin y-\cos y)`

It is required to simplify to a single trigonometry function using sin y and cos y.

To do this, use trigonometry identity:

`\cot y=(\cos y)/(\sin y)`

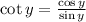
Hence, the expression can be written as:

`\begin{gathered} (1-\cot y)/(\sin y-\cos y)=(1-(\cos y)/(\sin y))/(\sin y-\cos y) \\ Rewrite\text{ 1 as }(\sin y)/(\sin y)\text{:} \\ =((\sin y)/(\sin y)-(\cos(y))/(\sin(y)))/(\sin(y)-\cos(y)) \end{gathered}`

Simplify the numerator:

`((\sin y-\cos(y))/(\sin(y)))/(\sin(y)-\cos(y))`

Simplify the expression further:

`(\sin y-\cos y)/(\sin y(\sin y-\cos y))`

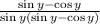
Cancel out common factors in the denominator and numerator:

`\frac{\cancel{\sin(y)-\cos(y)}}{\sin(y)(\cancel{\sin(y)-\cos(y)})}=(1)/(\sin(y))`

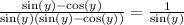
Hence, the required answer is 1/sin(y).