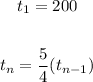Question

it says write an explicit and a recursive equation for the table bellow and it must work for each of the entries in the table

Answer 1

You use the next formula to get a explicit equation for a geometric sequence:

`a_n=a_1\cdot r^(n-1)`

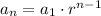
In this case you use as the first data 2000 (term when n=1).

r is the common ratio between each term.

To find r you divide each term into the previous term as follow:

`\begin{gathered} (2000)/(1600)=(5)/(4) \\ \\ (2500)/(2000)=(5)/(4) \\ \\ (3125)/(2500)=(5)/(4) \\ \\ (3906.25)/(3125)=(5)/(4) \end{gathered}`

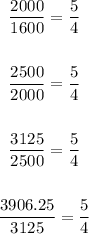
Then, you get the next explicit equation: writen in two different forms

`\begin{gathered} t_n=2000\cdot((5)/(4))^(n-1) \\ \\ t_n=(2000\cdot5^(n-1))/(4^(n-1)) \end{gathered}`

------------------------------------------

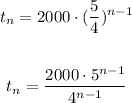
For the recursive formula you have the next:

Where tn-1 is the previus term

For the given sequence:

`\begin{gathered} t_1=200 \\ \\ t_n=(5)/(4)(t_(n-1)) \end{gathered}`